Backpropagation (역전파)
- 최적의 parameter 값을 찾기 위해 cost에 대한 입력층의 기울기를 계산하는 것
- 출력층의 기울기부터 계산하여 역으로 전파하기 때문에 Backpropagation;역전파 라고 함
- Chain Rule (합성함수의 미분법) 사용
Backpropagation in a Single Layer
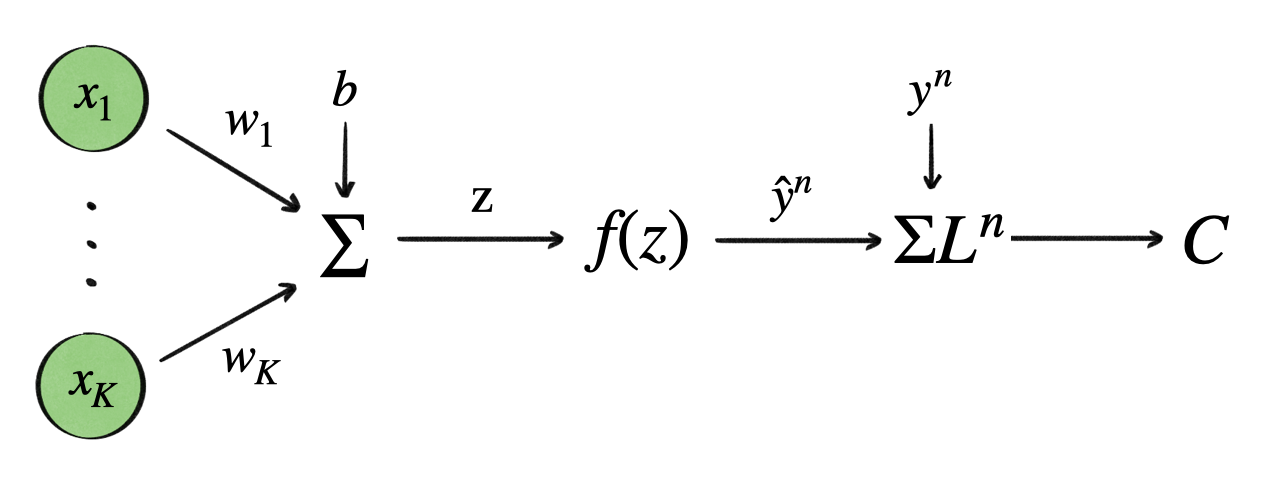
1. forward pass → weighted sum, activation function(sigmoid)
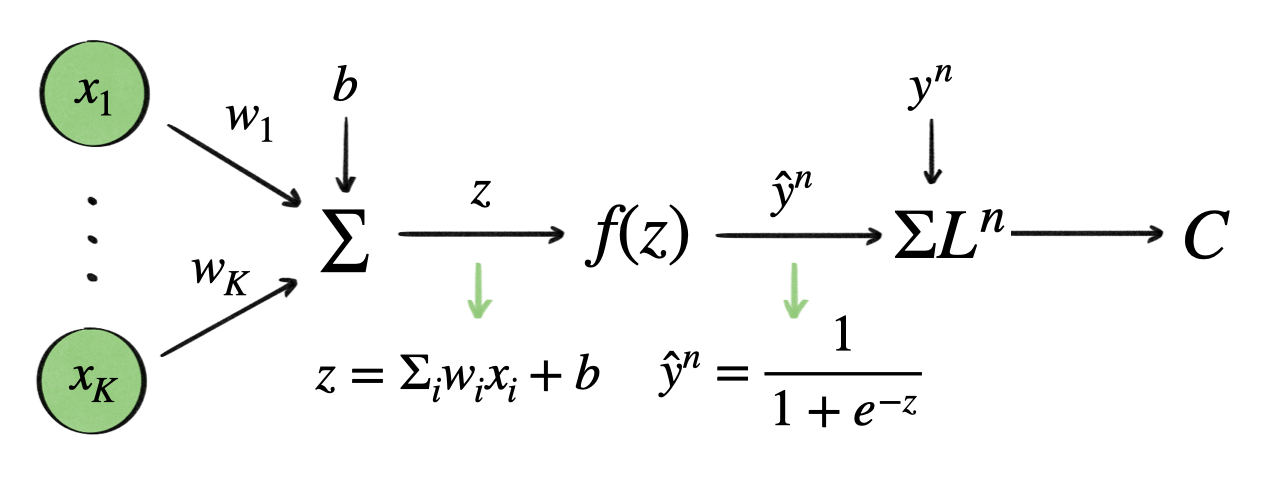
2. cost function → MSE
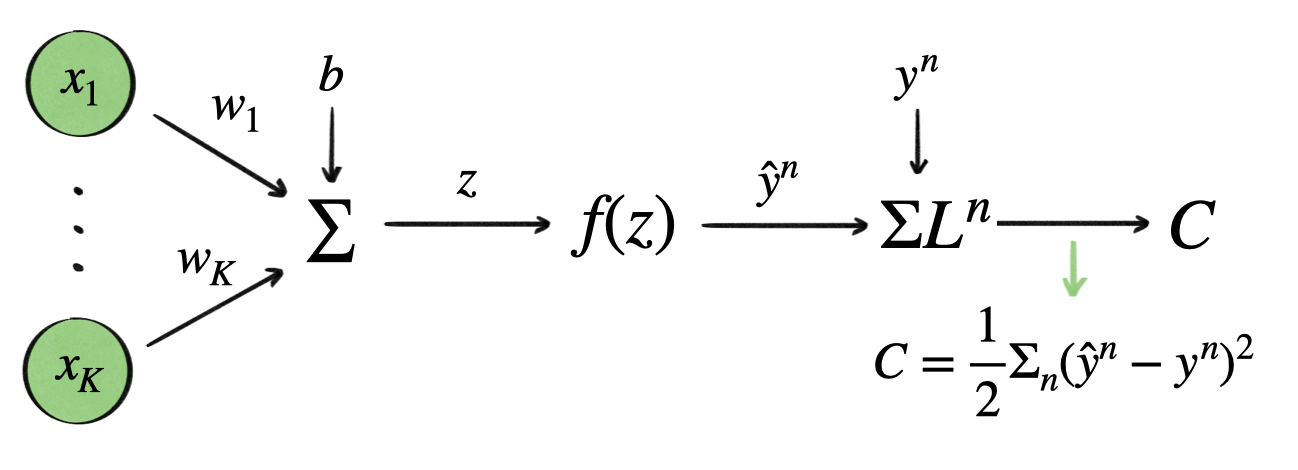
3. backpropagation
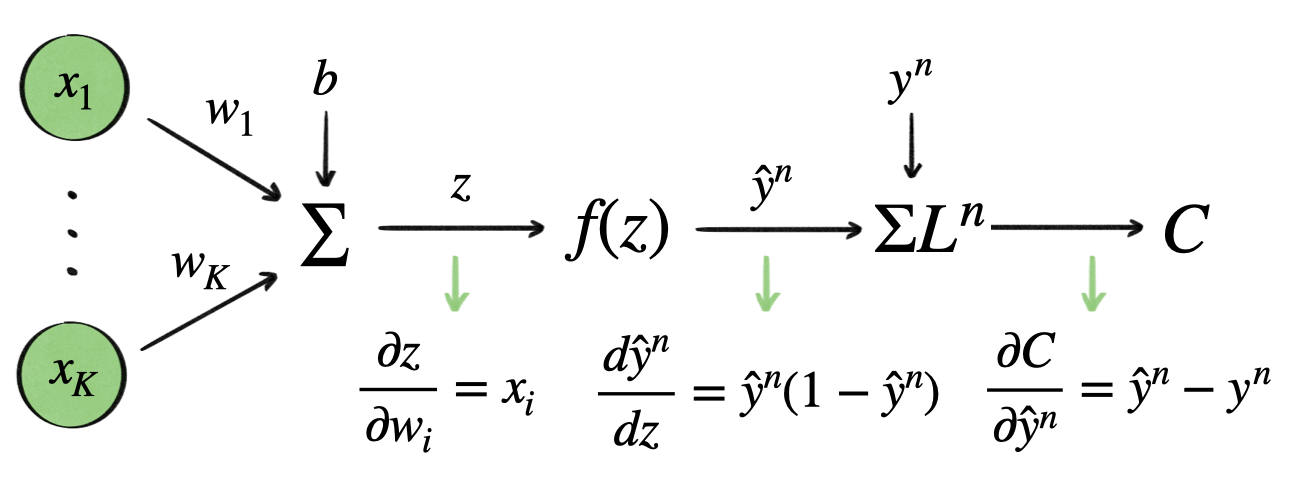
→ Chain Rule
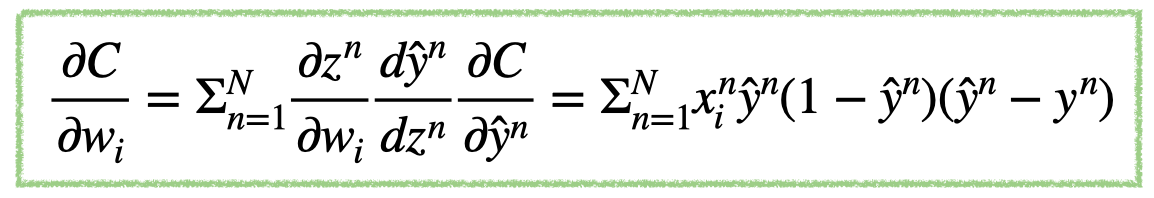
- $\frac{\partial C}{\partial w_i}$ : 3개의 함수로 이루어진 합성함수
- 해당 함수의 기울기를 구하기 위해 합성함수의 미분법인 Chain Rule 적용
- 위 식을 이루고 있는 값들은 $x_i^n$(input), $\hat{y}^n$(output), $y^n$(target) 으로 forward pass 때 계산된 값
Why Backpropagation Is an Efficient Way to Calculate Gradients
- Matrix 연산을 수행하기 때문에 parameter 값들을 동시에 update
- Backpropagation은 forward pass 때 구한 값들의 사칙연산으로 이루어져 있어, 메모리에 저장된 값들을 더하고 곱하는 식의 연산만 수행
'🌐 Jero's Wiki > Deep Learning' 카테고리의 다른 글
| Weight Initialization (0) | 2024.05.11 |
|---|---|
| Regularization (1) | 2024.04.26 |
| Likelihood & MLE (2) | 2024.04.21 |
| Gradient Descent (0) | 2024.04.17 |