목차
Gradient Descent (경사 하강법)
- loss function(손실함수) 값이 최소가 되는 방향으로 parameter 값을 update 하는 것
- 최소가 되는 방향 = Gradient 반대 방향
- 쉬운 구현성 및 높은 확장성, 거의 모든 최적화 문제에 적용 가능함
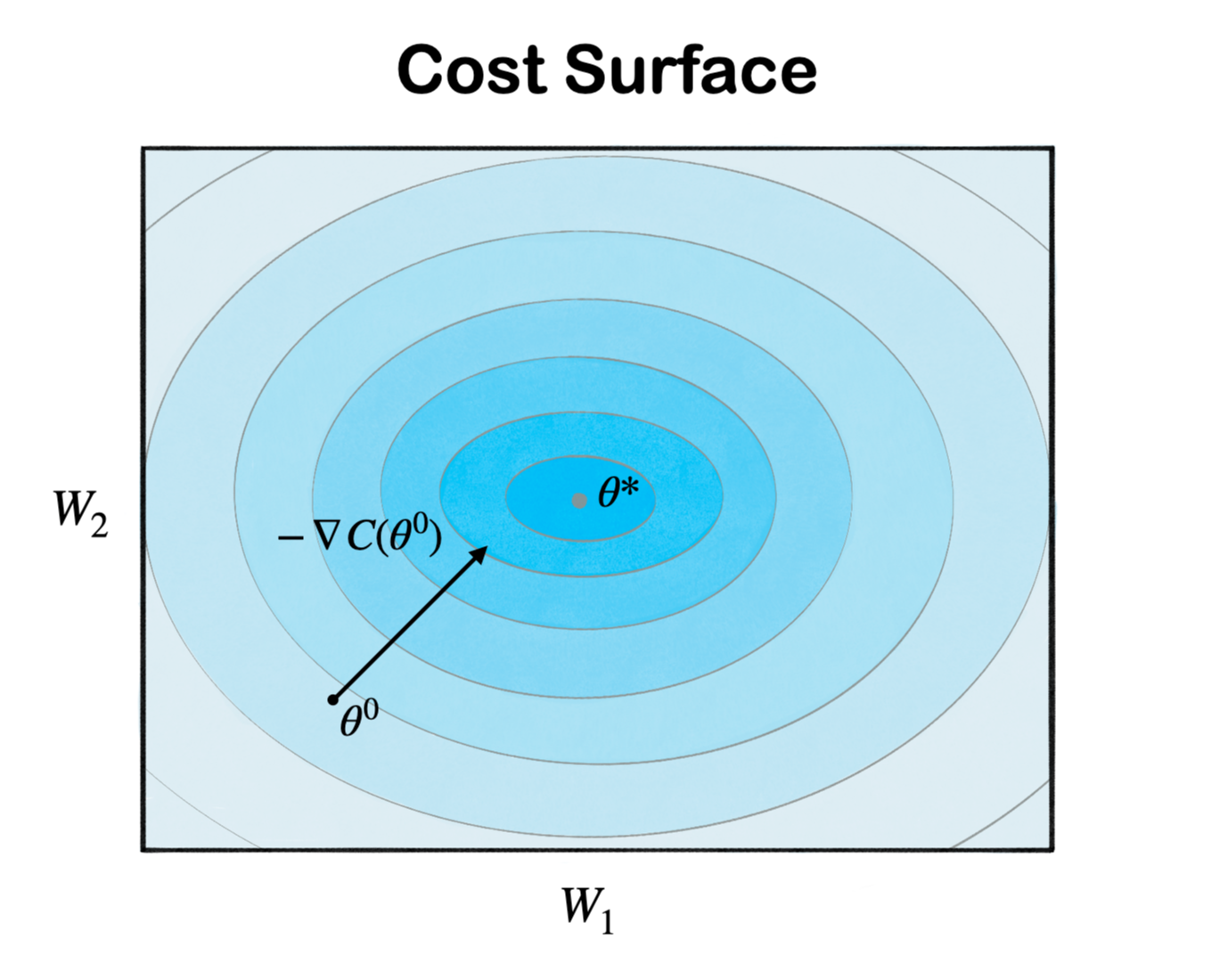
- starting point = $\theta^0$ → randomly pick !
- $\theta^0$ 에서 negative gradient 방향으로 이동 → $-\nabla C(\theta^0)$
- $\theta = (W_1, W_2), \ \nabla C(\theta^0)=\begin{bmatrix} \frac{\partial C(\theta^0)}{\partial W_1} \\ \frac{\partial C(\theta^0)}{\partial W_1} \end{bmatrix}$
Gradient Descent on Batch Size
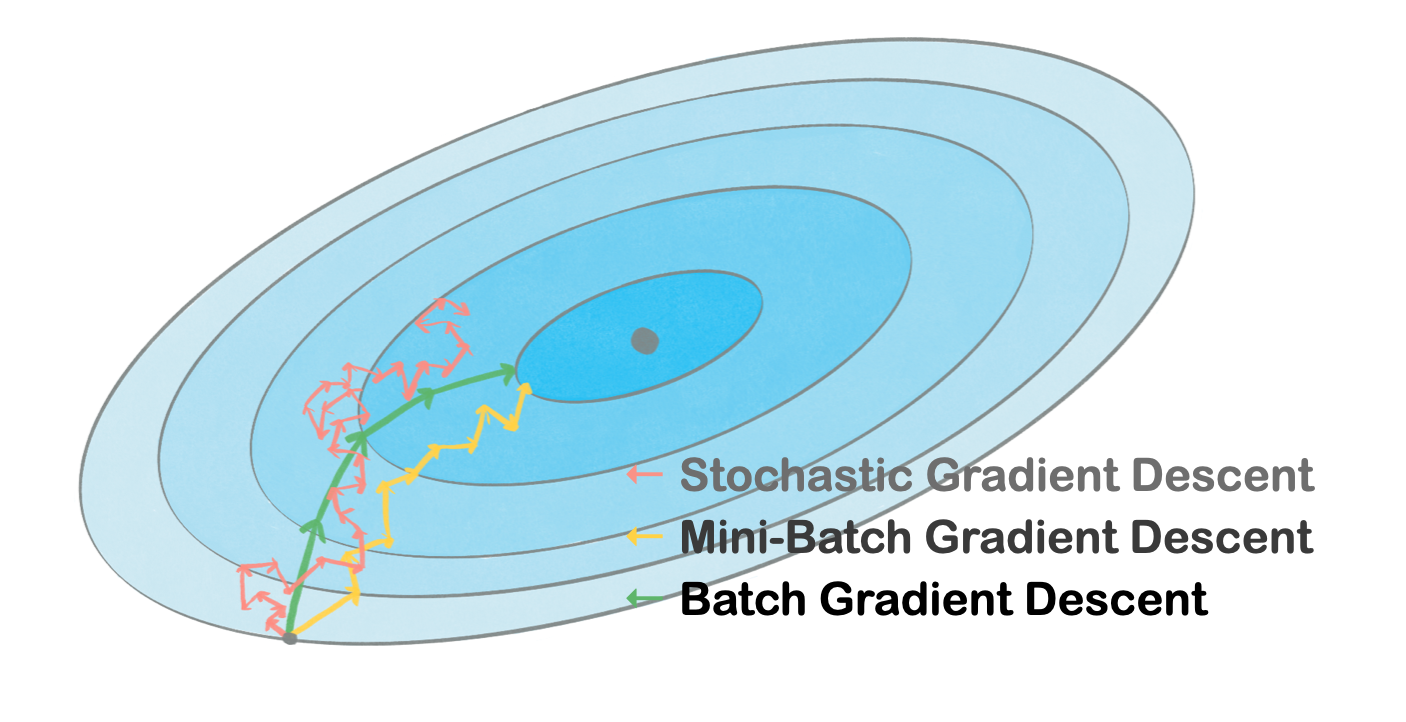
Batch Gradient Descent, Batch Size = 전체 훈련 데이터 개수
- 한 epoch 당 한번의 parameter update 진행
- 안정적인 최적화 경로 탐색 → outlier의 영향이 적음
- 낮은 일반화 성능
Stochastic Gradient Descent, Batch Size = 1
- 한 epoch 당 여러 번의 parameter update 진행
- 불안정한 최적화 경로 탐색 → outlier에 민감
- 높은 일반화 성능
Mini-Batch Gradient Descent, Batch Size = mini-batch 개수 (hyperparameter)
- mini-batch 수만큼 선택된 데이터를 가지고 gradient descent 진행
- SGD 보다 noise에 강해 안정적인 최적화 경로 탐색이 가능하고, BGD 보다 높은 일반화 성능을 기대
- 이상적인 mini-batch 값을 한번에 찾지 못할 수 있음
Why Small Batch Size Generalization Is Stronger
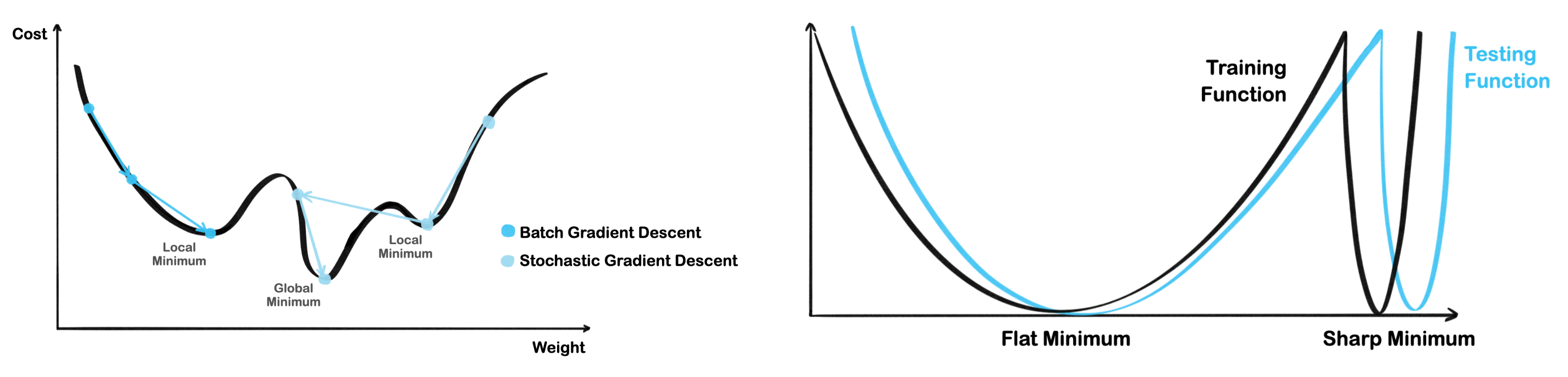
- Small Batch 일수록 Sharp Minimum에서 쉽게 벗어나며 noise에 둔감한 Flat minimum에 수렴
- Large Batch 일수록 Sharp Minimum 수렴 가능성 증가해 일반화 성능 감소
- Loss function의 작은 변화에도 민감한 Sharp Minimum은 Flat Minimum에 비해 일반화 성능 떨어짐
'🌐 Jero's Wiki > Deep Learning' 카테고리의 다른 글
| Weight Initialization (0) | 2024.05.11 |
|---|---|
| Regularization (1) | 2024.04.26 |
| Likelihood & MLE (2) | 2024.04.21 |
| Backpropagation (1) | 2024.04.18 |
Gradient Descent (경사 하강법)
- loss function(손실함수) 값이 최소가 되는 방향으로 parameter 값을 update 하는 것
- 최소가 되는 방향 = Gradient 반대 방향
- 쉬운 구현성 및 높은 확장성, 거의 모든 최적화 문제에 적용 가능함

- starting point = $\theta^0$ → randomly pick !
- $\theta^0$ 에서 negative gradient 방향으로 이동 → $-\nabla C(\theta^0)$
- $\theta = (W_1, W_2), \ \nabla C(\theta^0)=\begin{bmatrix} \frac{\partial C(\theta^0)}{\partial W_1} \\ \frac{\partial C(\theta^0)}{\partial W_1} \end{bmatrix}$
Gradient Descent on Batch Size

Batch Gradient Descent, Batch Size = 전체 훈련 데이터 개수
- 한 epoch 당 한번의 parameter update 진행
- 안정적인 최적화 경로 탐색 → outlier의 영향이 적음
- 낮은 일반화 성능
Stochastic Gradient Descent, Batch Size = 1
- 한 epoch 당 여러 번의 parameter update 진행
- 불안정한 최적화 경로 탐색 → outlier에 민감
- 높은 일반화 성능
Mini-Batch Gradient Descent, Batch Size = mini-batch 개수 (hyperparameter)
- mini-batch 수만큼 선택된 데이터를 가지고 gradient descent 진행
- SGD 보다 noise에 강해 안정적인 최적화 경로 탐색이 가능하고, BGD 보다 높은 일반화 성능을 기대
- 이상적인 mini-batch 값을 한번에 찾지 못할 수 있음
Why Small Batch Size Generalization Is Stronger

- Small Batch 일수록 Sharp Minimum에서 쉽게 벗어나며 noise에 둔감한 Flat minimum에 수렴
- Large Batch 일수록 Sharp Minimum 수렴 가능성 증가해 일반화 성능 감소
- Loss function의 작은 변화에도 민감한 Sharp Minimum은 Flat Minimum에 비해 일반화 성능 떨어짐
'🌐 Jero's Wiki > Deep Learning' 카테고리의 다른 글
| Weight Initialization (0) | 2024.05.11 |
|---|---|
| Regularization (1) | 2024.04.26 |
| Likelihood & MLE (2) | 2024.04.21 |
| Backpropagation (1) | 2024.04.18 |